La segmentation est un exercice répandu, et qui présente un intérêt dans de nombreuses disciplines. Elle peut être appliquée dans des domaines et des secteurs d’activité très divers tels que la santé, l’industrie, les sciences humaines ou dans les directions d’entreprise, dans les départements marketing ou financier par exemple. Dans cet article, nous allons nous focaliser sur une méthodologie générique s’accommandant à l’hétérogénéité de la plupart des cas d’utilisation. La première partie sera consacrée à la description du processus et la seconde à son implémentation.
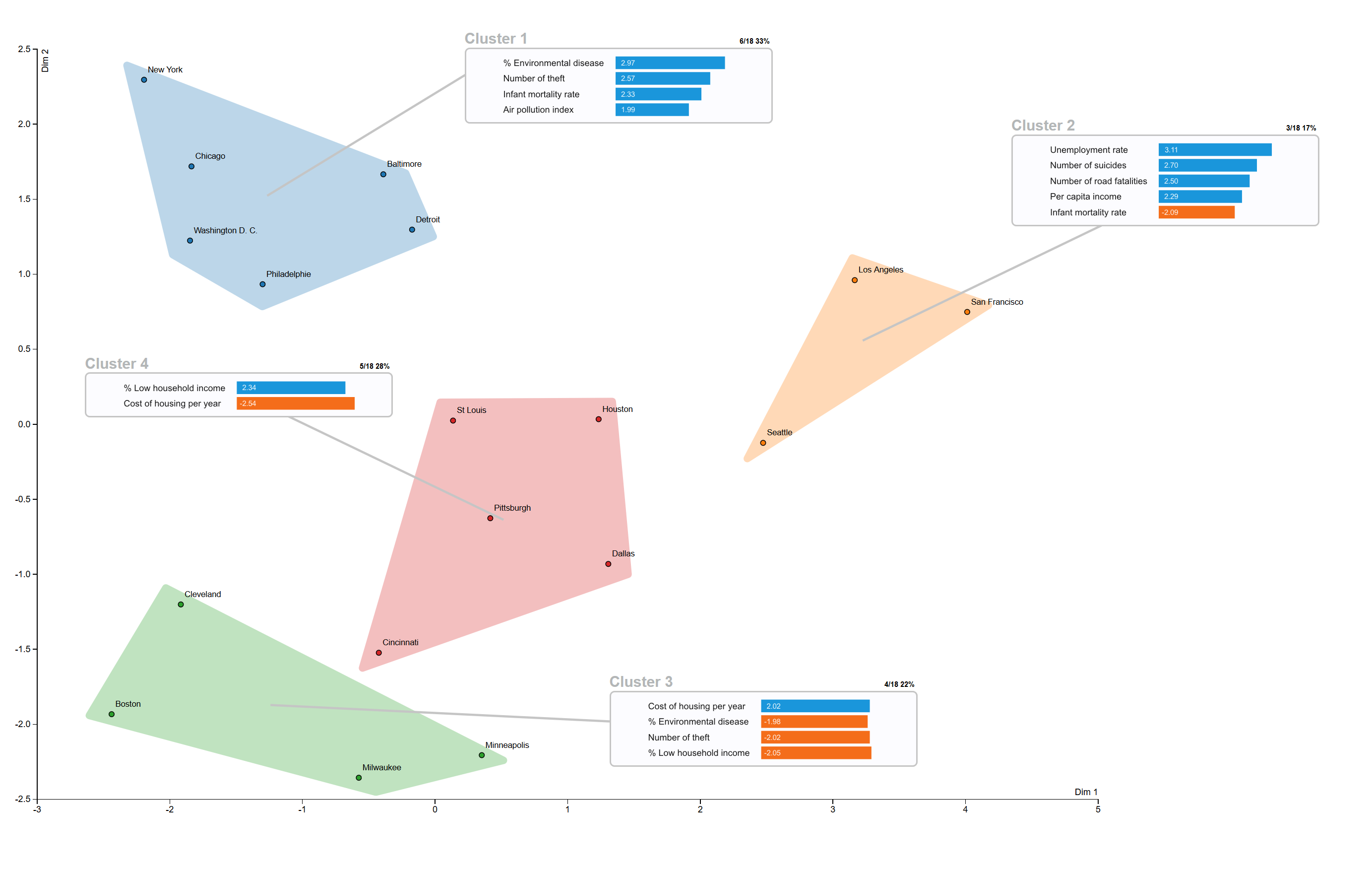
Exemple de segmentation de ville Américaines basée sur des données sociaux économique vue interactive ici (graphique élaboré en d3.js)
La segmentation est, par définition, le regroupement et la caractérisation d’observations dans des ensembles homogènes appelés communément « clusters ». Les recherches et travaux sur la question montrent néanmoins que la segmentation reste un exercice difficile : en raison notamment de sa nature qui peut se révéler arbitraire. Il existe une très grande panoplie d’algorithme permettant de séparer et regrouper des observations (classification non supervisée), et le choix de l’un par rapport à un autre n’est pas forcément évident. C’est également le cas du choix des variables à sélectionner, en quoi une variable représente et/ou est pertinente pour répondre au besoin de l’analyse ? Ces interrogations légitimes n’empêchent pas de produire une segmentation de qualité. Il est néanmoins nécessaire d’avoir conscience de ces nombreux biais afin d’exclure toute interprétation ou analyse erronées.
Dans le cadre d’une première approche, nous allons nous inspirer de la méthodologie proposée par le livre « Statistique exploratoire multidimensionnelle » (Dunod, Paris, 1995 ISBN 2100028863).
Elle est effectuée en plusieurs étapes :
- Réduction de dimension
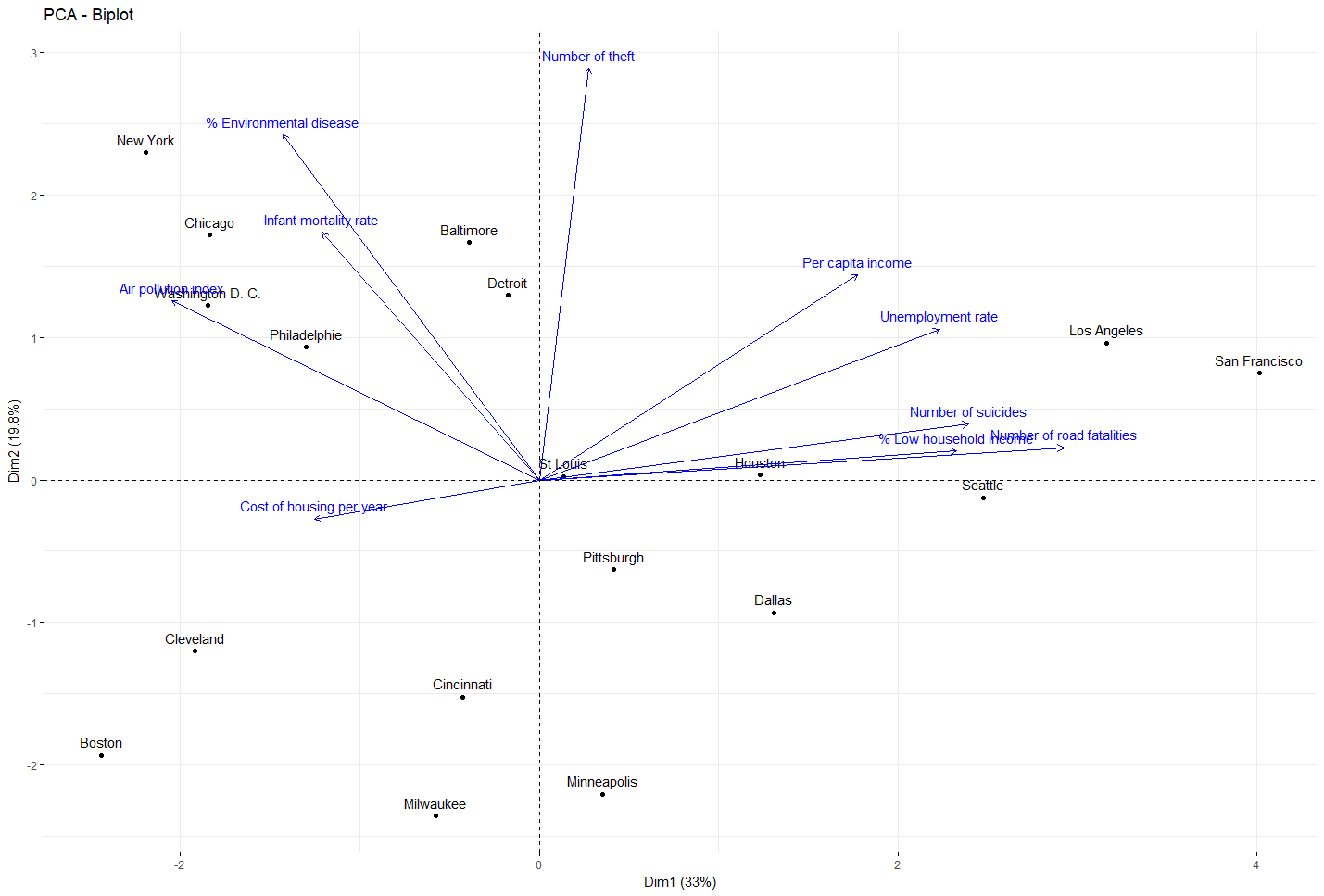
La réduction de dimension est l’exercice qui consiste à compresser l’information des données de grande dimension, en un nombre de dimension réduite. Il existe différentes méthodes de réduction, chacune d’entre elles présentent des avantages et des inconvénients. L’Analyse en Composante Principale (ACP) est ici la méthode employée. Cet algorithme utilise le paradigme de la corrélation pour réduire en dimensions un dataset. L’utilisation de la corrélation présente l’avantage de rendre l’interprétation des résultats plus aisée et intelligible. Bien que cette méthode soit assez élémentaire, elle est particulièrement recommandée et efficace pour visualiser des données multidimensionnelles, tout en ayant une perte d’informations quantifiable et contrôlée.
- Classification non-supervisée
Les algorithmes non-supervisés peuvent se baser sur différentes métriques : entropie, distance, densité. L’objectif recherché reste néanmoins toujours le même : Séparer des observations en des ensembles homogènes.
La classification Ascendante Hiérarchique (CAH) ici utilisée, consiste dans un premier temps à affecter une classe par observations et par la suite à regrouper progressivement les classes entre elles selon le critère de dissimilarité choisie. Elle est appliquée directement sur les coordonnées de L’ACP précédemment générées.
Le choix du nombre de clusters
La détermination du nombre optimal de clusters dans un dataset est un problème fondamental pour le clustering. Il n’existe pas de théorie qui résout de manière définitive et absolue cette problématique. Le nombre optimal de clusters garde une part de subjectivité. En effet l’évaluation des similarités, varie avec plus ou moins d’intensité en fonction de la méthode utilisée. Néanmoins, certaines de ces méthodes sont aujourd’hui consensuellement acceptées et couramment utilisées.
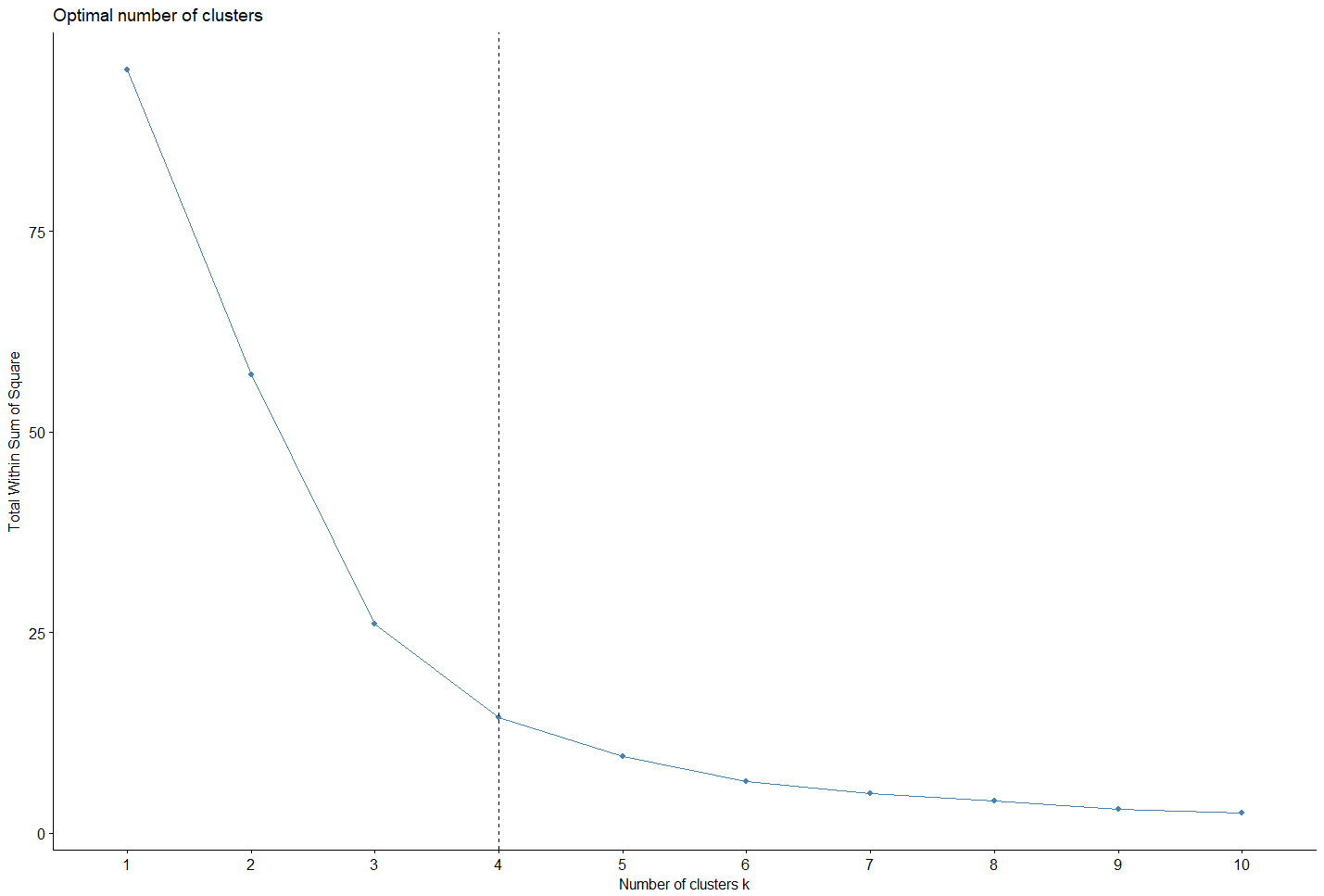
La Méthode d’Elbow est sans doute la méthode la plus utilisée pour la simplicité de son implémentation et pour son caractère accessible.
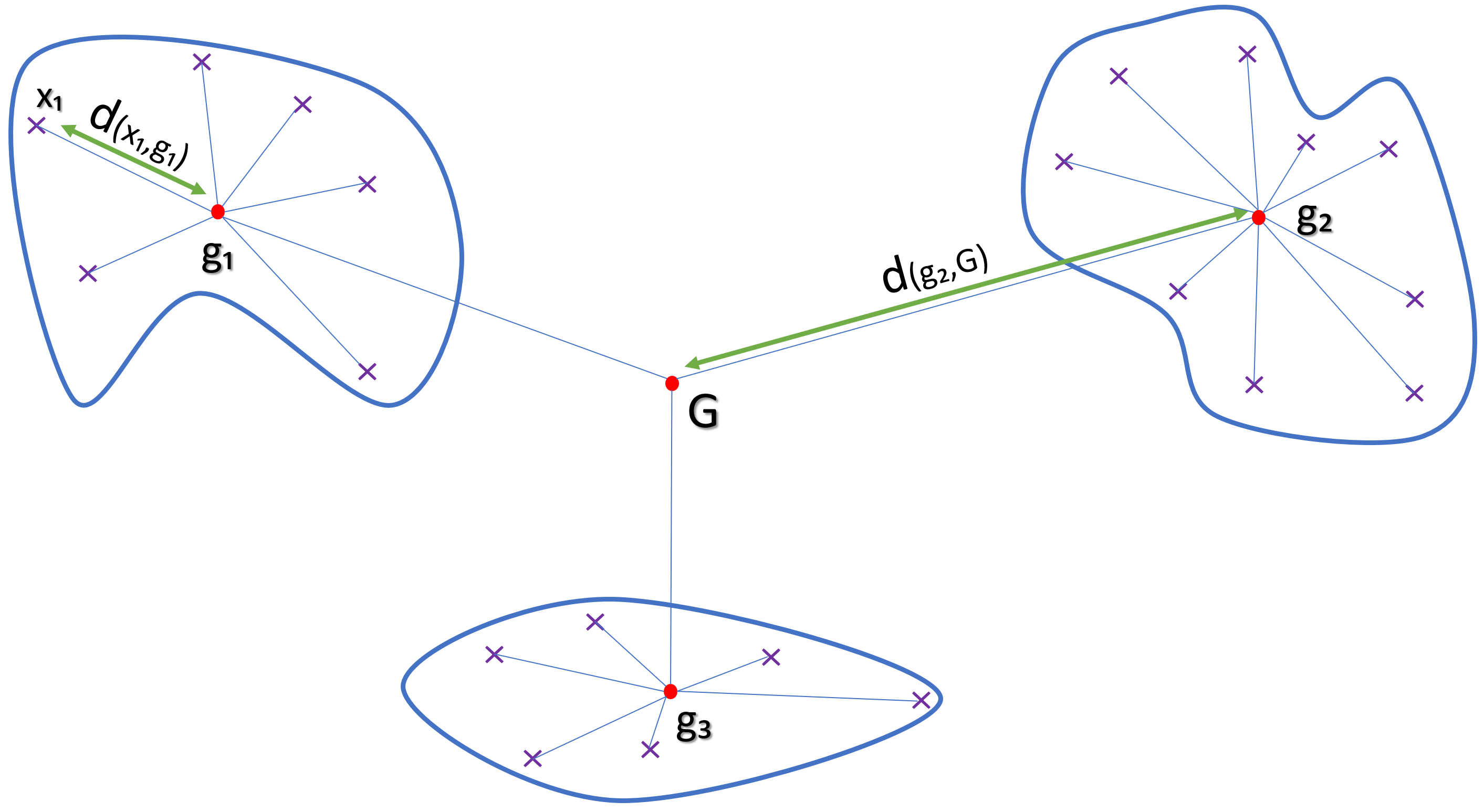
La technique consiste à exécuter l’algorithme de clustering plusieurs fois avec une valeur « k » du nombre de clusters différentes à chaque fois {2, 3, 4, etc…}. Pour chaque exécution est calculée l’inertie intra cluster, pour chaque cluster :
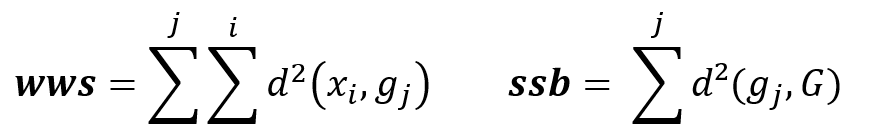
WWS : Within cluster Sum of Squares – inertie intra cluster
SSB : Sum of Squares Between cluster – inertie inter cluster
d(xi,gi) : Distance entre les points xi et les centres de gravité gi
L’objectif étant de minimiser l’inertie intra cluster (wws), cela revient également à maximiser l’inertie inter cluster (ssb) car inertie total du nuage de point étant la somme Totalinertie = wws + ssb
La valeur k du nombre de clusters à retenir est lorsque la décroissance de l’inertie entre deux valeurs successives de k se stabilise.
Intérêt d’appliquer la classification non-supervisée sur les résultats de l’ACP.
Il peut paraitre à première vue assez déconcertant d’appliquer la méthode de clustering directement sur les résultats de l’ACP et non sur les données brutes elles-mêmes. Pourtant cette façon de faire, possède aussi bien un intérêt pratique que théorique.
La combinaison des analyses procurent une visualisation indisponible. Dans le cas contraire, on peut ainsi avoir une idée des positions relatives des observations et des classes les unes par rapport autre mais également de leur dispersion et de leur silhouette.
Autre avantage, la possibilité de sélectionner un nombre restreint de dimensions générées par l’ACP. Cela afin de prendre en considération uniquement les dimensions qui possèdent un taux de variance expliqué élevées et délaisser les dimensions résiduelles, se préservant ainsi de potentielles fluctuations aléatoires indésirables. En se focalisant sur l’information la plus pertinente, nous améliorons de facto la qualité des partitions.
Du point de vue théorique, la stabilité des résultats reste garantie du fait que la somme des valeurs propres (inertie totale des dimensions sélectionnées) de L’ACP est égale à la somme des indices de niveau de la classification ascendante hiérarchique CAH (méthode de Ward).
Cet enchaînement vient également pallier un phénomène qui a cours en grande dimension : the Curse of Dimensionality (fléau de la dimension). Le concept est développé par Richard Bellman dans les années 60, dont l’idée consiste à dire qu’à nombre d’observations égales, plus on ajoute de dimensions, plus nous générons, et ce de manière exponentielle, du vide dans l’espace multidimensionnel. La manipulation de données en grande dimension rend alors le concept de distance (au sens euclidien du terme) progressivement dénuée de sens. Par conséquent, toute technique de regroupement basée sur la distance peut conduire à des résultats sous-optimaux.
- Caractérisation des clusters
Etape souvent négligée, dans ce genre d’exercice, la caractérisation des clusters représente pourtant, dans bien des cas, la valeur ajoutée du procédé.
La phase de clusterisation permet de regrouper des individus homogènes entre eux, mais elle n’indique en rien en quoi ces ensembles se ressemblent ou au contraire se distingue.
De nouveau, il existe plusieurs méthodes pour comparer les clusters les uns par rapport aux autres. Les tests statistiques utilisés sont souvent des tests de comparaison de moyennes basées sur des hypothèses de distribution des variables (Student, Normal…) D’autres utilisent la densité ou en encore des calculs plus sophistiqués.
Implémentation
Afin d’illustrer ce mécanisme, nous allons nous intéresser à segmenter certaines grandes villes américaines sur plusieurs critères : sociaux, économiques, démographique etc… dans le but de caractériser la notion de « bien-être » dans ces villes.
La procédure précédemment décrite a été codée en R et en JavaScript « D3.js » pour une meilleure visualisation. Le dataset et le code complet sont disponible ici.
Première etape:
Installation et importation des libraires et chargement des données.
library(FactoMineR)
library(factoextra)
library(ggplot2)
library(ggrepel)
library(DT)
library(jsonlite)
df=read.csv("wellness.csv", sep=";",dec=",",
row.names = 1, header= TRUE,
check.names=FALSE)
Deuxième étape:
Réduction de dimension avec l’ACP, et visualisation des résultats.
res_acp = PCA(df, scale.unit=TRUE, ncp=ncol(df), graph=F) df_acp=as.data.frame(res_acp$ind$coord) fviz_pca(res_acp, col.var ="blue")Afficher les résulats
Troisième étape:
Clusterisation en utilisant l’algorithme de la CAH. Elle est effectuée sur les données de l’ACP sur un nombre restreint de dimension tout en ayant precedement calculer le nombre de cluster optimal
alpha= 0.20
opt_calc=fviz_nbclust(df_acp[,c(1,4)], hcut, method = "wss")
for ( i in 1:10){
if(opt_calc$data$y[i+1]/opt_calc$data$y[1]<alpha){
nb_optimal=i+1
break
}
}
fviz_nbclust(df_acp[,c(1,4)], hcut, method = "wss")+geom_vline(xintercept = nb_optimal, linetype = 2)
cluster=cutree(CAH, nb_optimal)
cluster=as.data.frame(cluster)
df_cluster=cbind(df_acp,cluster)
Afficher les résulats
Quatrième étape:
Caractérisation des clusters avec un z-test (suppose que les variables sont distribuées selon la loi normal)
z.test = function(k, g){
n.k = length(k)
n.g = length(g)
Sk=((n.g-n.k)*var(g))/((n.g-1)*n.k)
zeta = (mean(k) - mean(g)) / sqrt(Sk)
return(zeta)
}
threshold=0.975
threshold.val=qnorm(threshold)
cluster_info <- data.frame(matrix(nrow=ncol(df)))
temp=data.frame()
df_c=cbind(df,cluster)
for ( j in 1:nrow(unique(cluster))){
cat("\n","cluster ", j, "\n", "\n", "\n" )
for (i in 1:ncol(df)) {
statistic=z.test(subset(df_c[,i], cluster==j),df_c[,i])
temp=rbind(temp,statistic)
if (statistic >=threshold.val || statistic <= -threshold.val) {
cat(colnames(df)[i],":",statistic[1],"\n")
}
}
colnames(temp)=paste("cluster",toString(j[1]) , sep=" ")
cluster_info=cbind(cluster_info,temp)
temp=data.frame()
}
Afficher les résulats cluster 1 % Environmental disease : 2.971881 Infant mortality rate : 2.332093 Air pollution index : 1.992268 Number of theft : 2.574825 cluster 2 Per capita income : 2.288678 Unemployment rate : 3.111431 Infant mortality rate : -2.092907 Number of suicides : 2.704074 Number of road fatalities : 2.496167 cluster 3 % Low household income : -2.045789 Cost of housing per year : 2.021008 % Environmental disease : -1.979993 Number of theft : -2.022158 cluster 4 % Low household income : 2.336857 Cost of housing per year : -2.544205
Dernière étape:
Génération du json, pour la visualisation en D3.js
path_json="viz/outfile.json"
if (file.exists(path_json)) file.remove(path_json)
cat("{",'"features":',"[",file=path_json,append=TRUE)
for(i in 1:ncol(cluster_info)){
cat('{\n"cluster":','"',i,'",','\n','"vars"',": [",'\n',file=path_json,append=TRUE)
cluster_info=cluster_info[order(cluster_info[,i],decreasing = TRUE), , drop = FALSE]
for(z in 1:nrow(cluster_info)){
if(abs(cluster_info[z,i])>=threshold.val){
cat('{','\n','"label" :','"',rownames(cluster_info)[z],'",','\n','"value":',round(cluster_info[z,i],digit=2),'\n }',file=path_json,append=TRUE)
if(max(which(abs(cluster_info[,i])>=threshold.val))!=z) { cat(",",file=path_json,append=TRUE) }
cat('\n',file=path_json,append=TRUE)
}
}
cat("] \n } ",file=path_json,append=TRUE)
if(ncol(cluster_info)!=i) { cat(",",file=path_json,append=TRUE) }
cat("\n" ,file=path_json,append=TRUE)
}
cat("],",'"observations": [',file=path_json,append=TRUE)
res1=df_cluster[, c(1,2,length(df_cluster))]
res1=cbind(ENTRY=rownames(df_cluster),df_cluster[, c(1,2,length(df_cluster))])
colnames(res1) <- c("name","Dim_1","Dim_2","cluster")
row.names(res1)<- NULL
x <- toJSON(unname(split(res1, 1:nrow(res1))))
x=gsub("[[]", "", x)
x=gsub("[]]", "", x)
cat(x,file=path_json,append=TRUE)
cat("\n ] \n }",file=path_json,append=TRUE)
L’approche non-linéaire
Que cela soit pour l’ACP ou bien la CAH, la compression ou séparation des données est effectuée toujours de la même manière : linéairement. Il existe une autre catégorie d’algorithme qui permet de compresser l’information d’un dataset avec une approche différente.
L’un des plus célèbre, le T-SNE, proposé par Geoffrey Hinton et Laurens van der Maaten, utilise des métriques issus de la théorie de l’information, en ayant notamment recours à une vision probabiliste des distances entre les observations. Il est aujourd’hui très utilisé et peut s’avérer salutaire pour distinguer des patterns locaux pouvant être dissimulés par des caractéristiques particulières de densité et de dispersions d’un dataset.
Du fait de son approche non linéaire, l’algorithme ne conserve ni les distances, ni la densité, mais la proximité entre les observations est en revanche maintenu.
Essentiellement élaboré pour des datasets de grande dimension, il reste néanmoins gourmand en temps de calcul et possède un paramètre clé : la perplexité qui nécessite d’être correctement calibré.
Le T-sne est un algorithme non déterministe en le ré exécutant plusieurs fois, il est possible d’avoir des différences sur la silhouette globale ainsi que sur les positions relatives des clusters.
En revanche les observations affectées à un cluster ne changeront pas de manière radicale.
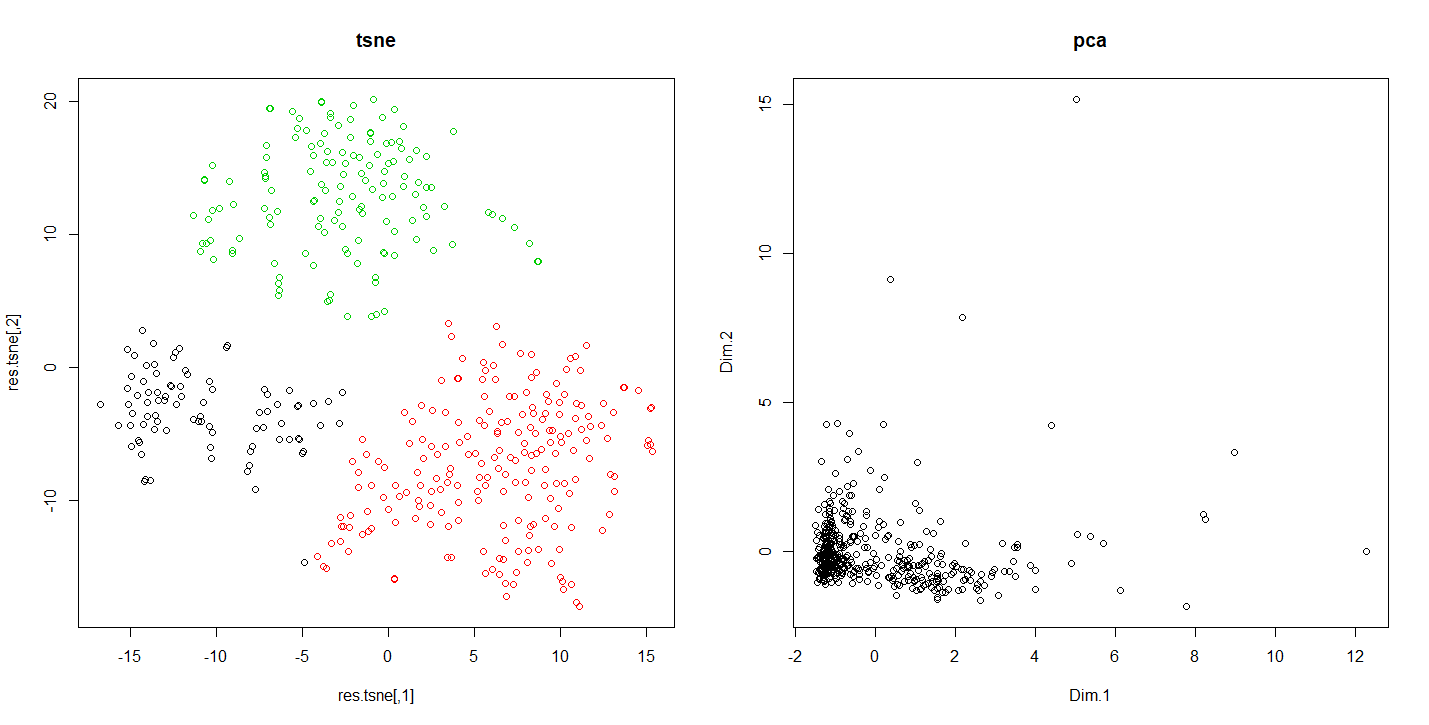
Afin d’illustrer la différence des résultats des réductions de dimension de l’ACP et du T-SNE. Nous allons appuyer sur un dataset représentant le comportement des clients dans une enseigne de la grande distribution.
Code R comparant les résultats du tnse avec l’acp
data=read.csv2("customers-data.csv",row.names = 1,header = TRUE)
data=data[,1:8]
res.pca = PCA(data, scale.unit=TRUE, ncp=ncol(df), graph=F)
res.tsne=tsne(scale(data),k = 2,max_iter = 500,epoch = 100,perplexity = 60)
km.tsne=kmeans(res.tsne,3)
par(mfrow=c(1,2))
plot(res.tsne,col=km.tsne$cluster,main="tsne")
plot(res.pca$ind$coord[,1:2],main="pca")
L’exécution de ce code nous montre comment en fonction de la méthode de réduction de dimension utilisé les résultats varient. Cela permet dans le cas présent de détecter des ensembles indiscernables autrement.
Différences de résultats entre le tsne et l’acp
Conclusion
La démarche présentée ici, nous montre une méthode pouvant être appliquée dans de nombreuses circonstances. Elle peut être ajuster en fonction des caractéristiques du dataset et présente l’intérêt d’une interprétation facilité par un ensemble d’indicateurs. Cela ne nous épargne pas en revanche, d’une vigilance particulière, au vu des écueils auxquelles nous pouvons être confronter dans ce genre d’exercice.
Réferences
[1] BellmanReferences, Richard. Dynamic programming. Courier Corporation, 2013.
[2] Benzécri, Jean-Paul. L’analyse des données. Vol. 2. Paris: Dunod, 1973.
[3] Maaten, Laurens van der, and Geoffrey Hinton. « Visualizing data using t-SNE. » Journal of machine learning research 9.Nov (2008): 2579-2605.